Ontology, graphs and turtles - Part II
In a previous article, I introduced the notion of ontology and knowledge graph.
Let’s go deeper into the concept and apply some technology to create an actual graph structure and eventually play with it.
At the end of this article, we well have parsed a triplestore in turtle format and created a graph structure in Go (based on gonum’s interface)
The triplestore
As explained in the last post, our knowledge database is a triple store. As a matter of example, I will rely on the ontology exposed by schema.org.
Schema.org is a collaborative, community activity with a mission to create, maintain, and promote schemas for structured data on the Internet, on web pages, in email messages, and beyond. Founded by Google, Microsoft, Yahoo and Yandex, Schema.org vocabularies are developed by an open community process […]. You can grab the complete ontology with this command:
The complete definition is available in turtle format and can be downloaded easily:
curl -O -s https://schema.org/version/latest/schemaorg-current-http.ttlParsing the store
Basic explanation of the parser
To parse the store, I am using the package gon3 from Andrei Sambra. Even though there is no license attached, Andrei allowed me to use it and to modify it for non-profit code.
I forked the repo to make some minor adjustments I needed for my experiments.
The entry point of the package is a Parser structure. Its purpose is to read a byte stream (io.Reader) and turn it into a functional structure called Graph. The Graph structure within the package is not representing all the edges. Still, it consists of an array of Triples (aka rdf graph):
// An RDF graph is a set of RDF triples
type Graph struct {
triples []*Triple
uri *IRI
}A Triple is a structure holding three Term. One is the subject, one is a predicate, and the last one is the object.
// see http://www.w3.org/TR/rdf11-concepts/#dfn-rdf-triple
type Triple struct {
Subject, Predicate, Object Term
}In the previous article, we saw that a term in RDF can be expressed in different types. As of today, the way to represent generic types in Go is to use interfaces. Therefore, a Term has an interface based definition:
type Term interface {
String() string
Equals(Term) bool
RawValue() string
}Two important objects are implementing the Term interface:
- IRI
- Literal
Generate the RDF Graph
If we glue all the concepts together we have the possibility to create a basic structure:
import "github.com/owulveryck/gon3" // Other imports omited for brevity
func main() {
baseURI := "https://example.org/foo"
parser := gon3.NewParser(baseURI)
gr, _ := parser.Parse(os.Stdin) // Error handling is omited for brevity
fmt.Printf("graph contains %v triples", len(gr.Triples()))
}Then we can test the plumbing with the file we downloaded from schema.org previously:
> cat schemaorg-current-http.ttl| go run main.go
graph contains 15323 triplesWe can check that roughly the number of triple matches what’s expected by counting the rdf separators from the file:
> cat schemaorg-current-http.ttl | egrep -v '^@|^$' | egrep -c ' \.$| \;$|\,$'
15329The numbers are not identical but alike (the grep command does not evaluate the literal and some punctuation may be wrongly counted)
Generating a Graph
Understanding the graph structure
We have an “RDF” graph in memory; sadly, this structure is not a directed graph. I mean that it is not de facto possible to navigate from nodes to nodes or to identify the edges.
To create a graph, the best option in Go is to rely on the abstraction created by gonum
In Gonum a graph is an interface that manages two objects fulfilling the Node and Edge such as:
type Graph interface {
Node(id int64) Node
Nodes() Nodes
From(id int64) Nodes
HasEdgeBetween(xid, yid int64) bool
Edge(uid, vid int64) Edge
}type Node interface {
ID() int64
}type Edge interface {
From() Node
To() Node
ReversedEdge() Edge
}Note: all comments have been removed for brevity. The full definition is available here
Once the graph objects are fulfilling those interfaces, it becomes possible to use all the graph algorithms that have been implemented by the gonum team. Please go to this link if you wish to learn more about the capabilities: pkg.go.dev/gonum.org/v1/gonum/graph#section-directories
Our graph structure
We will create a top-level structure that will act as a receiver for our graph. For the graph itself, we rely on the simple.DirectedGraph implementation provided by the gonum’s project.
So we have:
type Graph struct {
*simple.DirectedGraph
}Then we will create a function to create and fill our graph from our rdfGraph.
func NewGraph(rdfGraph *gon3.Graph) *Graph {
g := simple.NewDirectedGraph()
// ... fill the graph
return &Graph{
DirectedGraph: g,
}
}Structure of the graph
Remember that the rdf graph contains an array of triples. Each triple is a term.
The object of a predicate is the subject of another triple. For example:
schema:subject1 schema:predicate schema:object1 .
schema:object1 schema:otherPredicate schema:object2 .Would lead to the following graph:
This indicates a choice I’ve made: I want to produce a graph where its node corresponds to a subject declared inside the triplestore. Therefore, in the example, object2 is not a node because it is not defined as a subject to a sentence. It is relatively easy to change this behavior and reference other nodes, but let’s keep that apart.
Declaration of the node
The node object declaration is pretty straightforward. A node is a structure holding:
- an id
- a subject as seen before
- and a map of predicates and objects associated with the predicate.
type MyNode struct {
id int64
Subject rdf.Term
PredicateObject map[rdf.Term][]rdf.Term
}Adding a method ID() that returns an int64 makes it compatible with gonum’s Node interface.
Therefore it is possible to add it to a simple graph. So far, this codes compiles (but is useless):
g := &Graph{
DirectedGraph: simple.NewDirectedGraph(),
}
g.DirectedGraph.AddNode(&MyNode{})Declaration of the edge
Using the same principle, we create an Edge structure that holds two nodes From and To as well as a term that defines the edge.
type Edge struct {
F, T graph.Node
Term rdf.Term
}Therefore, this code compiles (but is useless):
g := &Graph{
DirectedGraph: simple.NewDirectedGraph(),
}
n0:=&MyNode{id:0}
n1:=&MyNode{id:1}
g.DirectedGraph.AddNode(n0)
g.DirectedGraph.AddNode(n1)
e := Edge{F: n0, T: n1}
g.SetEdge(e)We have created a graph with two nodes and an edge between them.
Parsing the rdf graph to generate our directed graph
The first thing we’ll do is to create a tree of terms. We do that thanks to a hash map. The key is a subject, and the value is another map. The map value’s key is a predicate and the value is an array of objects (remember that a predicate can point to several objects)
tree := make(map[gon3.Term]map[gon3.Term][]gon3.Term)But before parsing the rdf graph to fill the tree, we have to address a little gotcha. a Term is an interface. Therefore it is a pointer. Therefore in the rdf graph, if we consider two Terms t1 and t2 such as:
t1 := gon3.NewLiteral("bla")
t2 := gon3.NewLiteral("bla")t1 is different from t2 (even is their values are the same)
To address this, we will track a dictionary of terms indexed by their RawValue().
type Dict map[string]rdf.Term
func (d Dict) getOrInsert(t rdf.Term) rdf.Term {
//...
}Then we iter over the triples from our rdf graph to fille the tree and the dictionary.
for s := range rdfGraph.IterTriples() {
// ... fill dict and tree
}Note: for convenience, we will also set the dictionary as an attribute to our graph for later. The structure becomes:
type Graph struct {
*simple.DirectedGraph
Dict map[string]rdf.Term}We can now range over the tree, and create all the nodes in the graph for each subject:
for s, po := range tree {
n := &Node{
id: g.NewNode().ID(),
Subject: s,
PredicateObject: po,
}
g.AddNode(n)
reference[s] = n
}Note: once again, for convenience, we track the nodes in a hash map. This reference map has the subject as a key and the node as a value (its type is map[rdf.Term]*Node).
Finally, we loop once again through the tree to create the edges:
for s, po := range tree {
me := reference[s]
for predicate, objects := range po {
for _, object := range objects {
if me == to { // self edge
continue
}
to := reference[object]
e := Edge{ F: me, T: to, Term: predicate, }
g.SetEdge(e)
}
}
}Note: error handling is omited for brevity
Putting all together
Now that we have the graph builder ok, we can test it with the data from schema.org we downloaded earlier.
Let’s write a simple program that creates the graph and do a simple query. For example, we may want to get all the nodes directly linked to the PostalAddress in schema.org.
baseURI := "https://example.org/foo"
parser := rdf.NewParser(baseURI)
gr, err := parser.Parse(os.Stdin)
if err != nil {
log.Fatal(err)
}
g := graph.NewGraph(gr)
postalAddress := g.Dict["http://schema.org/PostalAddress"]
node := g.Reference[postalAddress]
it := g.To(node.ID())
for it.Next() {
n := it.Node().(*graph.Node) // need inference here because gonum's simple graph returns a type graph.Node which is an interface
fmt.Printf("%v -> %v\n", node.Subject, n.Subject)
}This prints the following output:
❯ cat schemaorg-current-http.ttl| go run main.go
<http://schema.org/PostalAddress> -> <http://schema.org/deliveryAddress>
<http://schema.org/PostalAddress> -> <http://schema.org/postalCode>
<http://schema.org/PostalAddress> -> <http://schema.org/servicePostalAddress>
<http://schema.org/PostalAddress> -> <http://schema.org/originAddress>
<http://schema.org/PostalAddress> -> <http://schema.org/addressCountry>
<http://schema.org/PostalAddress> -> <http://schema.org/location>
<http://schema.org/PostalAddress> -> <http://schema.org/billingAddress>
<http://schema.org/PostalAddress> -> <http://schema.org/addressLocality>
<http://schema.org/PostalAddress> -> <http://schema.org/postOfficeBoxNumber>
<http://schema.org/PostalAddress> -> <http://schema.org/streetAddress>
<http://schema.org/PostalAddress> -> <http://schema.org/address>
<http://schema.org/PostalAddress> -> <http://schema.org/addressRegion>
<http://schema.org/PostalAddress> -> <http://schema.org/gameLocation>
<http://schema.org/PostalAddress> -> <http://schema.org/itemLocation>If we check on schema.org’s website (https://schema.org/PostalAddress), we find those elements but in two different tables:
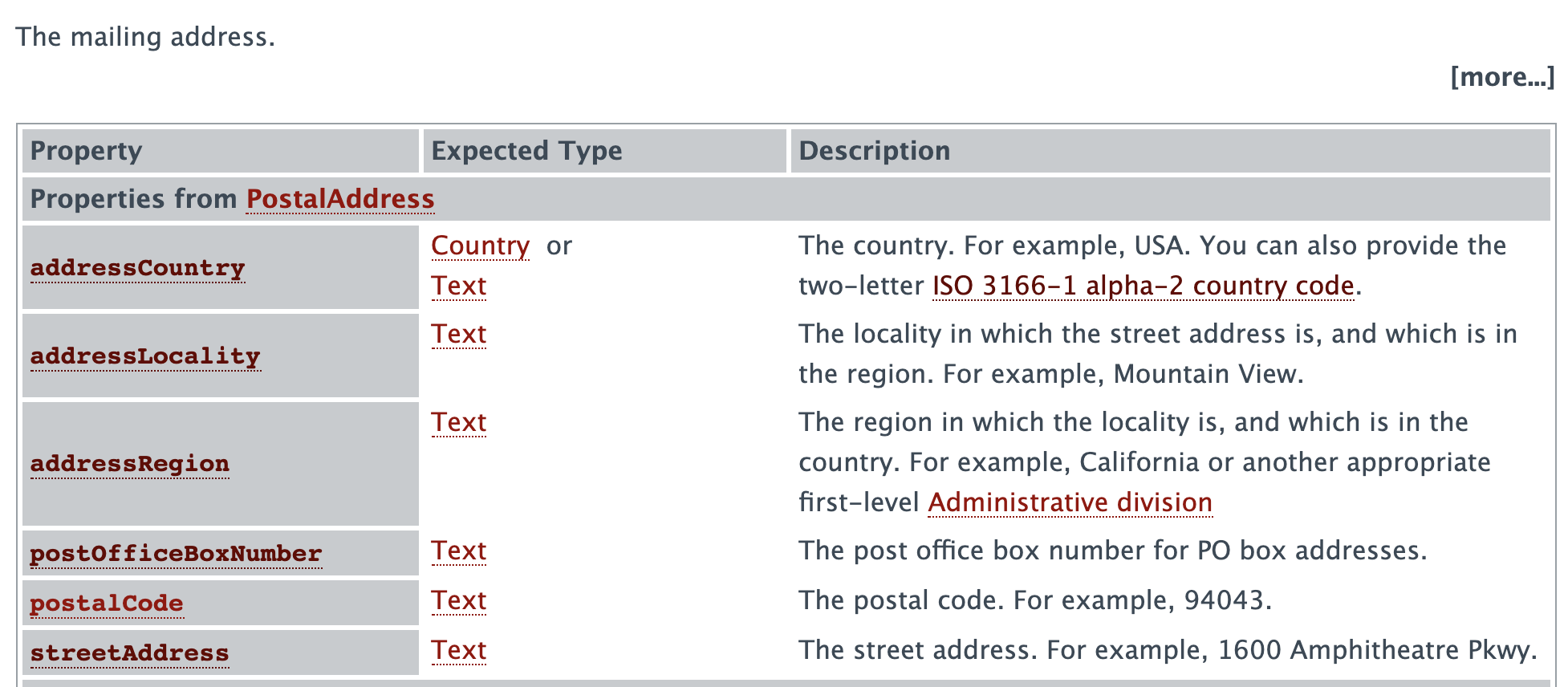
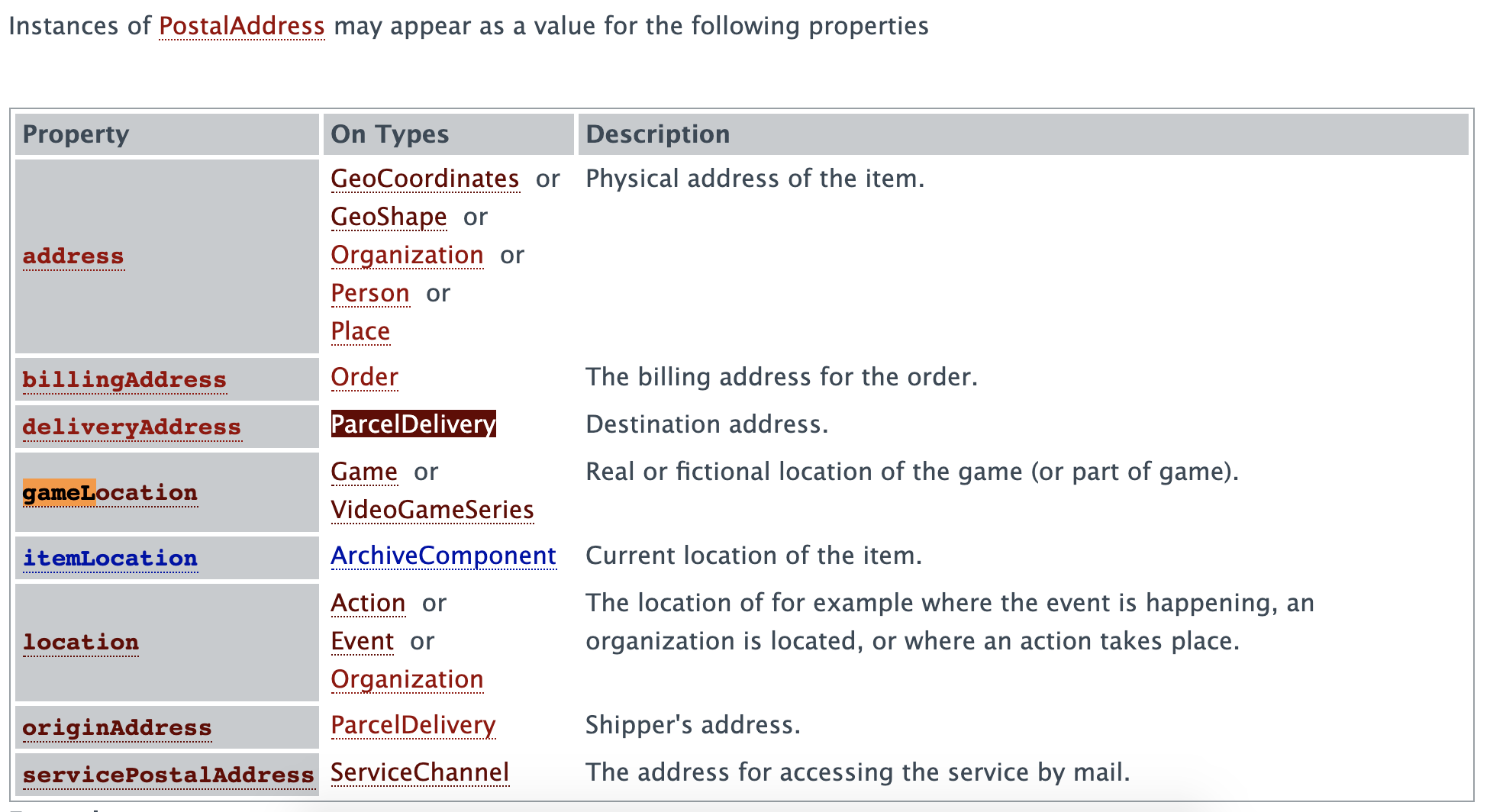
Remember, we are dealing with ontology; therefore, the link has a meaning. And this meaning has been set as an attribute of the edge. If we tweak the code to display the edge like this:
for it.Next() {
n := it.Node().(*graph.Node) // need inference here because gonum's simple graph returns a type graph.Node which is an interface
e := g.Edge(n.ID(), node.ID()).(graph.Edge)
fmt.Printf("%v -%v-> %v\n", node.Subject, e.Term, n.Subject)
}we obtain:
<http://schema.org/PostalAddress> -<http://schema.org/domainIncludes>-> <http://schema.org/addressRegion>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/billingAddress>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/servicePostalAddress>
<http://schema.org/PostalAddress> -<http://schema.org/domainIncludes>-> <http://schema.org/streetAddress>
<http://schema.org/PostalAddress> -<http://schema.org/domainIncludes>-> <http://schema.org/addressCountry>
<http://schema.org/PostalAddress> -<http://schema.org/domainIncludes>-> <http://schema.org/postOfficeBoxNumber>
<http://schema.org/PostalAddress> -<http://schema.org/domainIncludes>-> <http://schema.org/addressLocality>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/location>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/itemLocation>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/deliveryAddress>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/address>
<http://schema.org/PostalAddress> -<http://schema.org/domainIncludes>-> <http://schema.org/postalCode>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/gameLocation>
<http://schema.org/PostalAddress> -<http://schema.org/rangeIncludes>-> <http://schema.org/originAddress>Conclusion
We’ve built a graph structure in memory quickly. What’s important is not the structure by itself. The important is the perspectives it opens. So far, we have worked on schemas, but the semantics applies to the data itself. On top of that, the graph we have generated is reasonably generic. Therefore, the same principle could be used to store our knowledge graph within a persistent database such as dgraph or maybe neo4j.
In the next article, we will work with the graph and set up a template engine to create generic documentation of our knowledge graph using go template.
Meanwhile, you can fetch the code (which is not production-ready) on my github